Contents#
- Introduction
- Effective HP
- Applications
- "Stacking evasion has diminishing returns"
- Still, don't use IDW
- The other side
- A problem with IWS Exodia
- Heavy Ordnance Corps
- In conclusion
Introduction#
Evasion and accuracy stats are used to determine how often your dolls will hit, and how often they will get hit in combat. The formula for hit rate is pretty simple:
$$ \text{Hit rate}~(\%) = \frac{\text{ACC}}{\text{ACC}+\text{EVA}} \times 100\% $$But there are a number of interesting aspects to this. Let's plot this equation to get a visual.
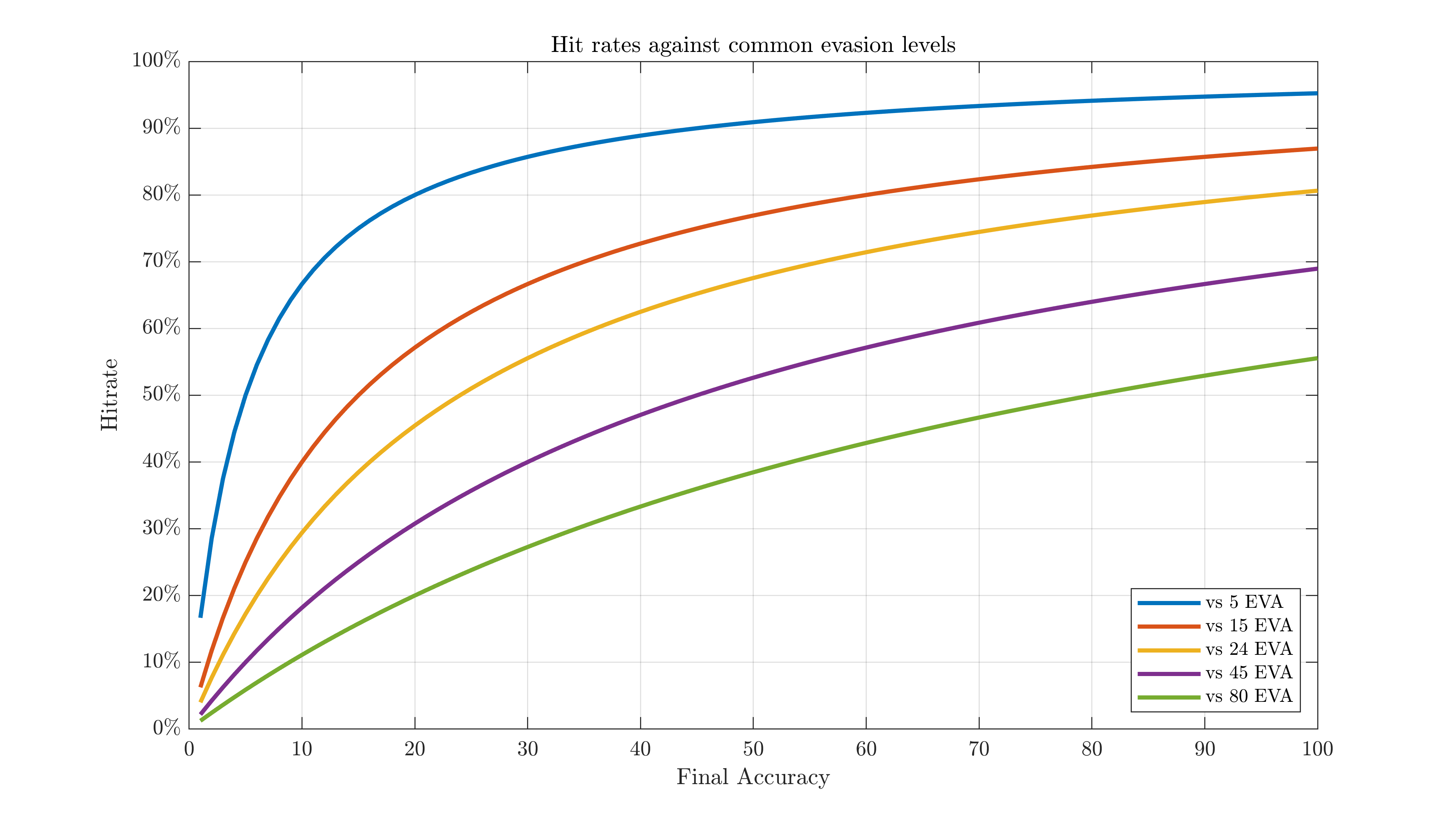
Hit rate increases rapidly at first, but will slow down the higher your accuracy is relative to enemy evasion. You can find specific enemy stats here. In 3D:
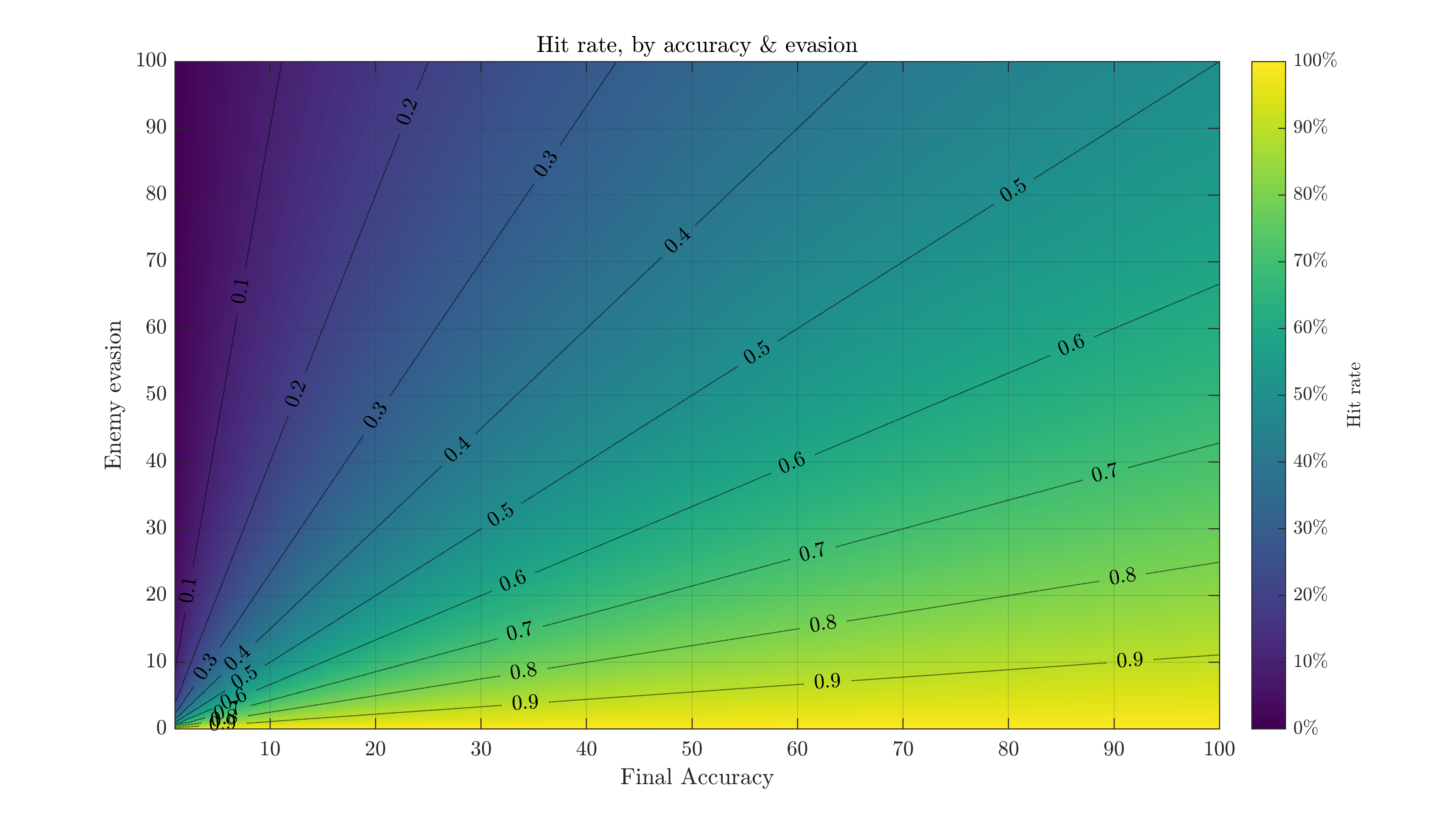
Find where your accuracy & the enemy's evasion meet, and the color is your chance of each bullet hitting. Warmer colors = more likely to hit, the reverse also works for the odds you'll get hit. Dodge chance is simply 1 minus the hit rate, or EVA/(EVA+ACC).
Example: the Centaurus (KCCO Archers) in Core 8 have 51 accuracy. A fully equipped lv115 UMP45 with a 56% evasion buff (Artillery aura) has 203 evasion. Each attack will then have a 51/(51+203)=51/254≈20.08% chance to hit her.
At night, your final accuracy gets a little more complicated1:
$$ \mathrm{ACC}_{\mathrm{Night}} = \left\lfloor \mathrm{ACC} \cdot (1 - 0.9 \cdot(1 - \mathrm{PEQ~correction})) \right\rfloor $$Where \( \lfloor x \rfloor \) is the floor function. A 100% PEQ will completely negate the night penalty, while no PEQ means you get the full 90% penalty. Sadly, enemies have their own little Night Vision chip and are not affected by this penalty. On your end, here's what this PEQ formula looks like:
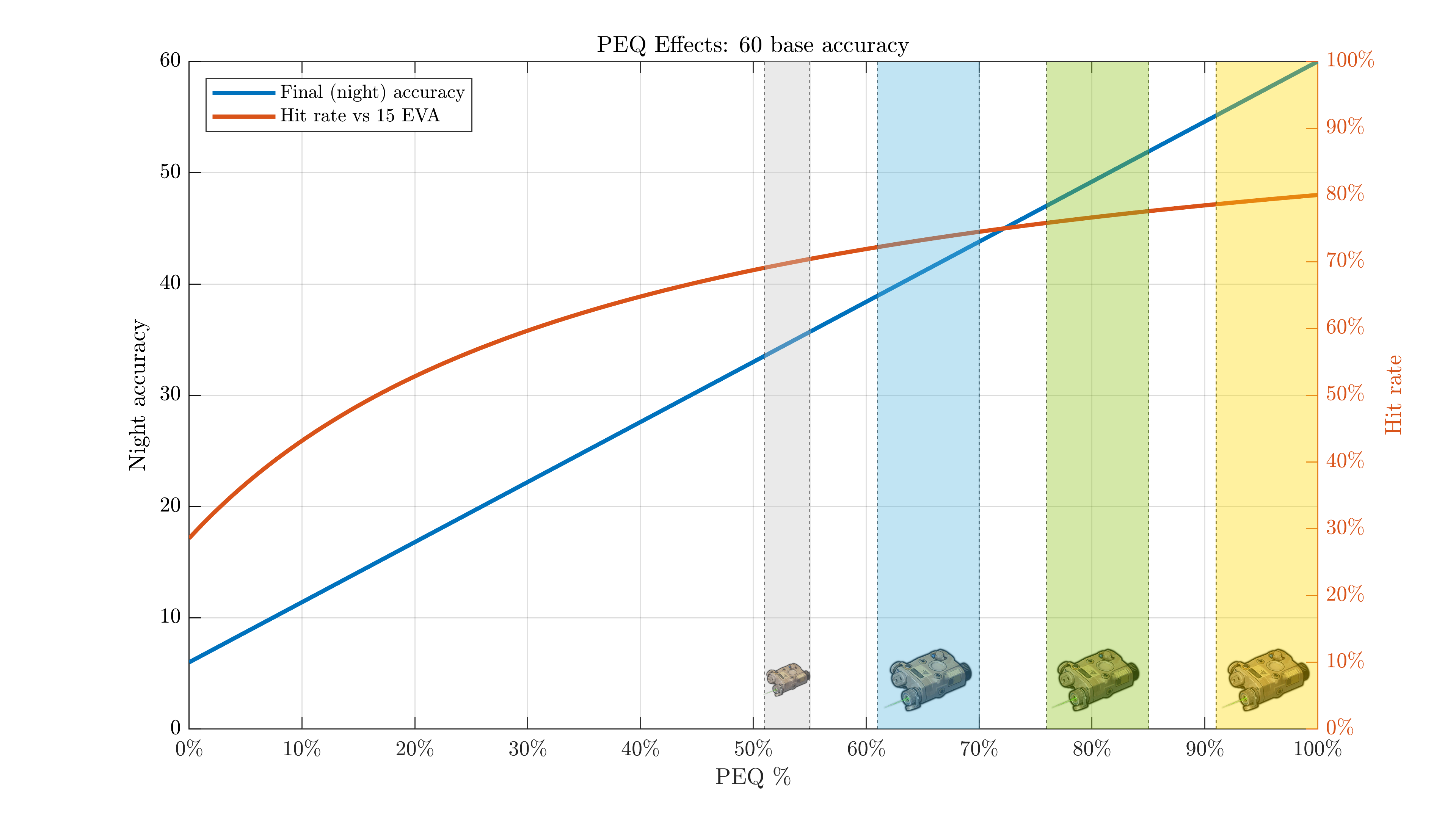
And you can probably see why calibrating gold PEQs isn't recommended: hit rate barely improves at that point, assuming your base accuracy is significantly above your target evasion. If you don't care about min-maxing theater CE, even green PEQs are good enough for most purposes.
This works both ways, for friendlies and enemies, with no minimum. Today, I'd like to go over a few less-obvious aspects of this.
1: That document is quite old, and a few bits are out of date. All dolls have 15 base AP now, and HOCs have a 40% hit rate floor (bonus: experimentally verified).
Effective HP#
$$ \mathrm{EHP} = \frac{\mathrm{HP}}{\mathrm{Enemy~hit~rate}} = \frac{\mathrm{HP}}{1-\mathrm{Dodge~chance}} $$Let's move away from talking about evasion and hit rates, and introduce another number: effective HP, or EHP for short. Consider a particularly bad shotgun with 1000 HP and 0 evasion. All attacks made will hit, so once enemies fire off 1000 damage you'll die. Now, suppose instead that shotgun had a bit more evasion, just enough to match that enemy's accuracy. On average, 50% of their shots will miss, requiring the enemy to attack for 2000 points of damage this time. EHP is a measure of how much HP a 0-evasion tank would need to last as long on average.
Effective HP is very nice to work with: twice the EHP, twice the survivability, twice as good. It also lets you compare units with significantly different HP/EVA distributions.
If you'd like to play around with this a bit, here's a calculator:
| Doll | HP | Final EVA | Enemy ACC |
|---|---|---|---|
| Doll #1 | |||
| Doll #2 |
| Doll | Dodge chance | EHP |
|---|---|---|
| Doll #1 | ?% | ? EHP |
| Doll #2 | ?% | ? EHP |
Applications#
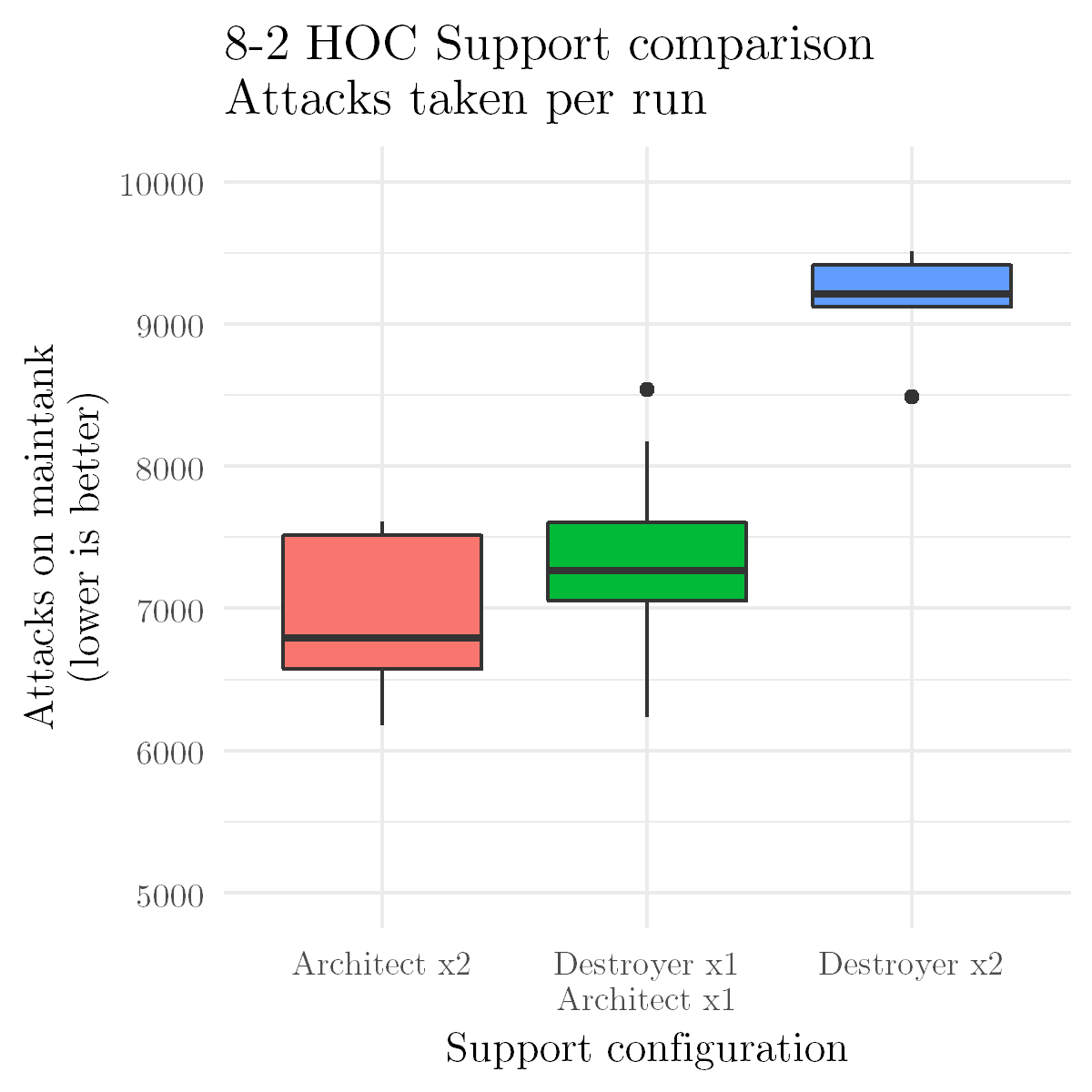
I've been collecting some data on the damage taken from 8-2 SF drag runs. The following chart shows the estimated number of total attacks the maintank took, by support configuration. Using one or two Architects significantly reduced the number of attacks that need to be tanked, lowering damage and speeding the grind up.
Repairing your maintank can be a pain, so it would be nice if you could last the whole run without doing so. If you have sufficient armor, you can reduce all damage to 1. Getting more EHP than the number of expected attacks taken should allow you to survive without any repairs. Let's say you have a friend or two with Architect support and assume you want to be able to survive 8k attacks. All spawns there have 20 accuracy, which makes this much easier. A few examples:
- lv96 L Aegis: 1309 HP, 66 EVA. It has \( \frac{1309}{20/(20+66)} = 5628~\mathrm{EHP} \). Not quite enough.
- Add Defend: \( \frac{1309}{20/(20+66\cdot 2)} = 9948~\mathrm{EHP} \), a 77% increase and enough EHP to survive with a decent safety margin.
- lv92 L Manticore: 1539 HP, 79 EVA. \( \frac{1537}{20/(20+79)} = 7618~\mathrm{EHP} \), or 13697 with Defend (+80%). Possibly survivable without Defend, but with Defend it's easy.
- lv93 L Nemeum: 932 HP, 50 EVA. Even with Defend, it has only 5592 EHP.
- Even a lv100 XL Tarantula, with 356 HP/88 EVA, has 1922/3489 EHP without/with Defend - with a decent chance at needing two repairs per run, I would not recommend these as a primary tank. Note that whatever you put on 7/8 takes far fewer attacks and only needs ~300-500 EHP, so they're perfectly fine in that position.
Or for more a more competitively-relevant example, here's a comparison between the force shielders against Dog/Archers. Assuming max level/100 affection/best exo & suppressor equipped, their EHPs against a Centaurus' 51 accuracy are:
| Configuration | Dodge chance (base) | Dodge chance (+100% EVA) | Effective HP (base) | Effective HP (+100% EVA) |
|---|---|---|---|---|
| MP5: T-Exo | 70.2% | 82.5% | 3037 | 5171 |
| MP5: SPEQ | 73.7% | 84.9% | 3441 | 5993 |
| MP5: SPEQ+buffed mod SPEQ | 74.4% | 85.3% | 3531 | 6158 |
| G36c: T-Exo | 69.1% | 81.7% | 3285 | 5546 |
| Thompson: T-Exo | 67.1% | 80.3% | 3617 | 6041 |
| Thompson: SPEQ | 68.1% | 81.0% | 3733 | 6277 |
Orthrus are a bit more accurate. Here's the same table with 143 enemy accuracy.
| Configuration | Dodge chance (base) | Dodge chance (+100% EVA) | Effective HP (base) | Effective HP (+100% EVA) |
|---|---|---|---|---|
| MP5: T-Exo | 45.6% | 62.7% | 1664 | 2424 |
| MP5: SPEQ | 50.0% | 66.7% | 1810 | 2715 |
| MP5: SPEQ+buffed mod SPEQ | 50.9% | 67.4% | 1842 | 2778 |
| G36c: T-Exo | 44.4% | 61.5% | 1824 | 2633 |
| Thompson: T-Exo | 42.1% | 59.3% | 2055 | 2921 |
| Thompson: SPEQ | 43.3% | 60.4% | 2097 | 3004 |
This doesn't account for tile differences or MP5's skill2, but it's useful to see how they all compare in base durability. Most interestingly, Thompson's large HP pool seems to outweigh her lower evasion, with the highest EHP across the board. More on that over here.
"Stacking evasion has diminishing returns"#
The above statement is incorrect.
You may have noticed that the Defend chip in the SF examples above gave rather substantial survivability increases, even with a Manticore whose base evasion was ~4x the enemy's accuracy. This is not some trick or fluke.
As your evasion gets higher and higher relative to enemy accuracy, your dodge chance will approach 100%. While this does mean changes in dodge chance will be smaller percentage point-wise, that's not actually the metric you should be looking at.
Your effective HP will be quite good with a 99% dodge chance, but adding "just" 1 percentage point to that takes you to 100% dodge chance where your EHP would be infinite. Not that you can actually get infinite EHP, but even consider the difference between a 90% dodge chance and 95% - you take half as many hits with a 95% dodge rate, and will live twice as long on average.
We can define a survivability increase like so:
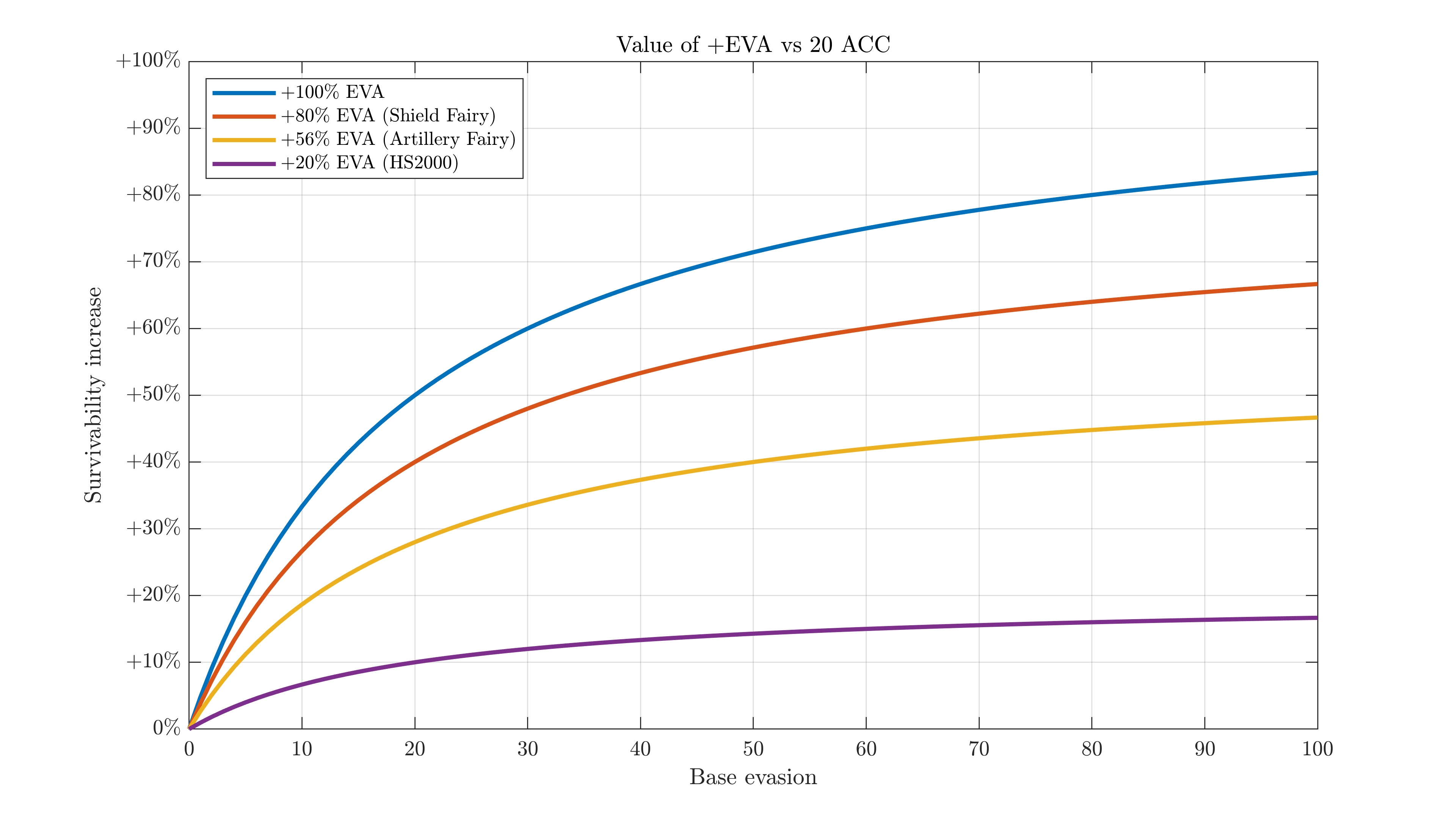
$$ \mathrm{Survivability~increase} = \frac{\mathrm{New~EHP}}{\mathrm{Old~EHP}} = \frac{\frac{\mathrm{HP}}{\mathrm{New~Enemy~hit~rate}}}{\frac{\mathrm{HP}}{\mathrm{Old~Enemy~hit~rate}}} = \frac{\mathrm{Old~Enemy~hit~rate}}{\mathrm{New~Enemy~hit~rate}} $$For a visual perspective, here's a chart of the gain in survivability (EHP) a few different EVA buffs give you against a 20-accuracy enemy, depending on what your evasion stat was beforehand.
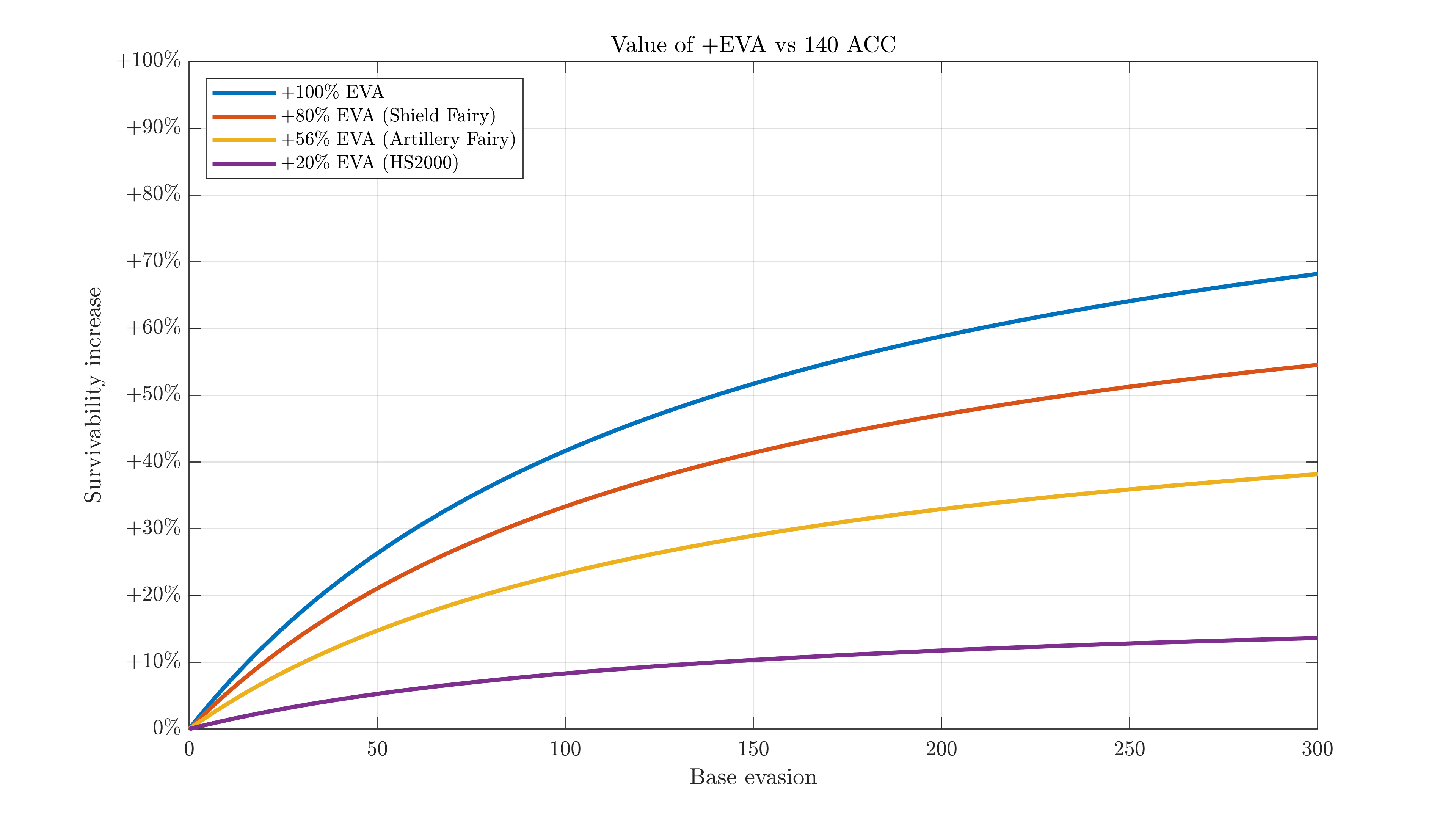
This scales about as expected if going against higher accuracies:
If you start with 0 evasion, evasion buffs obviously don't help you at all - 0*anything=0. With low base evasion, you gain very little survivability from this - there's not much of a difference between getting hit 98% of the time and 95% of the time. As your base evasion increases, the gain from this buff will increase, approaching a +100% EHP improvement for +100% EVA, +80% EHP for 80% EVA, and so on. If you want a bit more proof this does cap out: supposing some constant enemy accuracy a and a 100% EVA buff,
$$ \lim\limits_{\mathrm{EVA}\to\infty} \frac{\frac{a}{a+\mathrm{EVA}}}{\frac{a}{a+2\cdot\mathrm{EVA}}} = \lim\limits_{\mathrm{\mathrm{EVA}}\to\infty} \frac{a+2\cdot\mathrm{EVA}}{a+\mathrm{EVA}} = 2 $$(You can similarly show that an accuracy buff can never provide a larger DPS increase than the buff itself, i.e., a 100% ACC buff is at its absolute best a 100% DPS buff - which happens when your accuracy is near 0/enemy evasion is extremely large.)
Still, don't use IDW#
This shows that increasing evasion can do something, and there are no literal "diminishing returns" (if anything, it's the opposite). This does not show that this thing is useful, or that it is better than other things you could be doing (like increasing damage). Consider two theoretical options:
- Increase your SMG maintank's evasion by 300%, massively boosting their survivability against weaker enemies
- Increase your backline's DPS by 300%, killing all enemies before they get even a single attack off
Guess which one is more likely to reduce your damage taken better. Welrod was benched for a reason many moons ago when Px4 Storm was released. A number of especially scary attacks are surehit, and no amount of evasion will save you then (unless you're RO mod). It's also possible to cover survivability through other means, like with the skill of a Shield Fairy.
(If you don't care about minimizing damage and only need to win the fight, past some point you'll have enough evasion to get to the end anyways and further evasion buffs don't affect that outside of a minor consistency boost. This could be viewed as proper 'diminishing returns,' but I don't think this is a relevant perspective for most stuff outside of coalition drills.)
Experiment: Killing Strelets
Starting with a team skeleton of G41, Type95, and C-MS, let's try killing a Strelet mob and see how it works for varying combinations of three offensive/defensive buffs. To fill out the rest of the team, I'll use:
- Defensive support
- Shield Fairy
- El Fail
- Makarov
- Offensive support
- Command Fairy
- Mk23
- SAA
Tile differences, link protection, and various other factors make this rather unscientific. Strelets have low accuracy stats (here, 19), so evasion stacking is more viable. Other enemies like Cerynitis or SWAP SF can have 150+ accuracy, making evasion tanking substantially less effective. In normal combat you can also kite, significantly reducing the amount of time you're sitting there and taking attacks. Cross-ish formation for easy tile-fitting. Don't try this at home.

The teams with 0 or 1 defensive picks performed similarly well, but after that adding more enemy debuffs and party evasion was counterproductive - not only did fight time increase dramatically, but the damage taken also increased.
This is all against a very forgiving enemy with low accuracy. Stacking evasion against Doppelsöldners, Uhlans, Minotaurus, Cerynitis, and many more enemies will end very badly.
The other side#
Now, let's look at this from the other side. Enemies themselves have evasion, and you'd like to kill them as quickly as possible. The previous results are easy enough to invert - the higher your accuracy is relative to their evasion the less it matters - but I'll rework the chart anyways as it can help to have a visual.
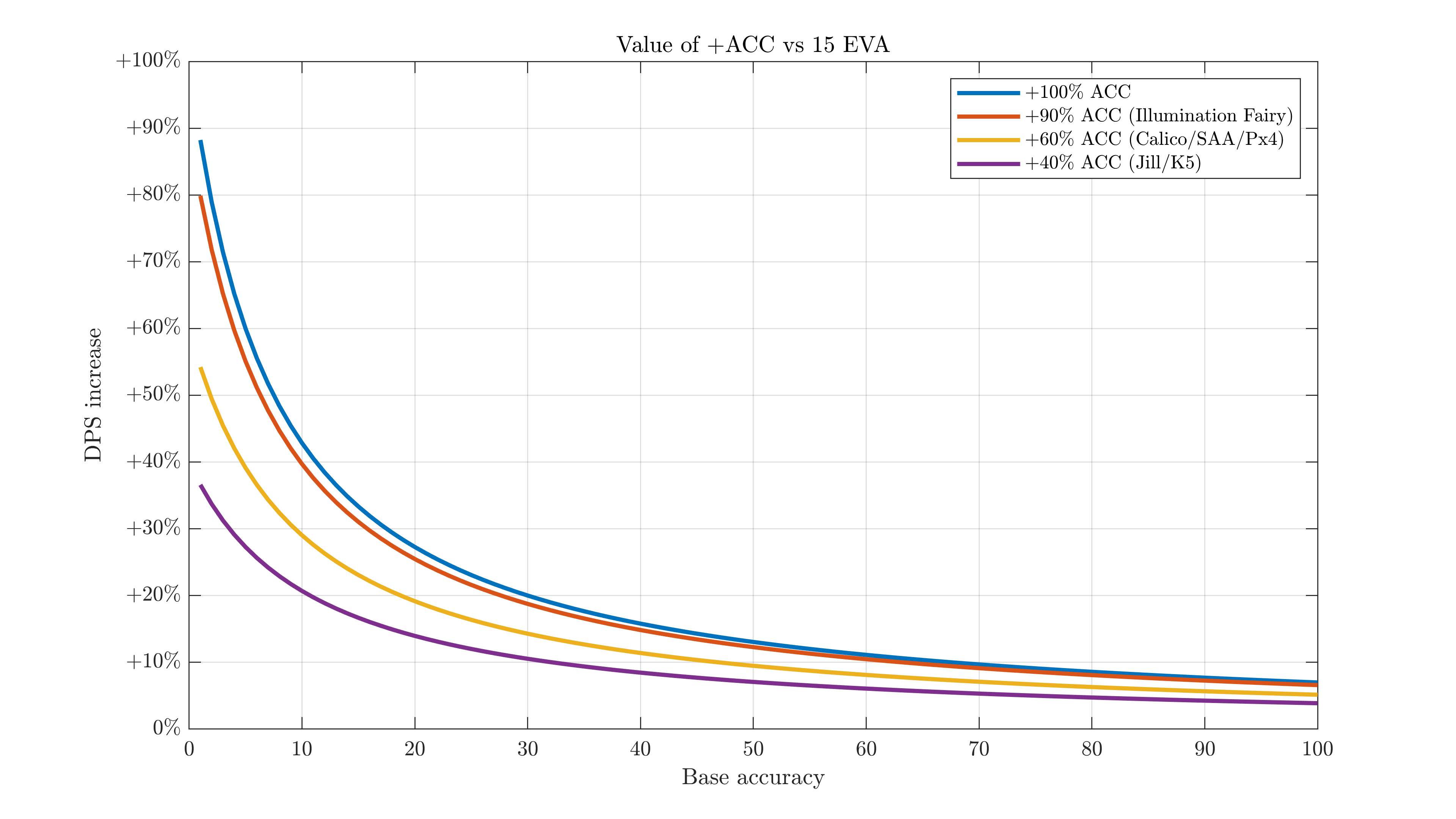
Here's the average DPS increase a few common accuracy buffs give, by your starting accuracy, against a 15-evasion enemy. If your base acc is double their evasion, even a 100% acc buff is reduced to a 20% DPS increase. Past 70 accuracy and this buff is only 1/10th as strong.
As you may expect, the equation for net DPS increase is just about the inverse of the survivability increase:
$$ \mathrm{DPS~increase} = \frac{\mathrm{New~hit~rate}}{\mathrm{Old~hit~rate}} $$Going from a 70% hit rate to a 80% hit rate is an 80%/70% = 1.1428 = 14.28% DPS improvement, on average.
If you ever wanted to know why SRS isn't very popular at day, this is it. She has a 60% FP/40% ACC selfbuff, and vs typical 15 evasion stuff that 40% acc is in the range of a 5% DPS boost given her 87 base ACC. A 1.6*1.05=68% net DPS buff isn't awful, but typical 5-stars have a 75% multiplier. It's even less if you have other accuracy sources. At night, she does better: 8 accuracy vs 15 evasion means a ~25% DPS boost from that same acc component, for a ~2x net skill DPS boost. But even then, there are other options like M200/Type88/4 Shiki/heavy acc tiles.
On the other hand, accuracy tends to be given in much larger amounts. It's easy enough to get 100-150% acc from tiles, and another 60% or so from a fairy. At night, rifles will have more around 10 base accuracy, so they gain much more from accuracy buffs. This is nowhere near 1:1 with the same % damage buff, but it can be a respectable bonus.
A problem with IWS Exodia#
Giant Eagle Assault. Initial CD 6s/Skill CD 16s
In return for decreasing rate of fire by 35%, increase damage by 180% for 10 seconds.
IWS captured the hearts of many players back around launch, as her skill had big numbers. A popular idea was to pair her with 4 ROF-buffing HGs, and use IWS as the sole damage-dealer. Even on paper its DPS output wasn't great, so this idea has largely fallen by the wayside. However, exodia-style formations do see some use with other dolls instead of IWS (M4 exodia in SC ranking, Type88 exodia in PL ranking).
IWS' skill works out to an [(1-0.35)*2.8]-1=82% net DPS buff ignoring any frame shenanigans, which is slightly above the typical 5-star standard (of 75%, but also nowhere near as much as the FP buff could lead you to think). One major problem with this type of formation is link protection - each bullet can kill at most one enemy link. If IWS has more than enough FP to oneshot a given 5-linked enemy, even a single bullet missing will leave them alive at one link and need another shot to actually kill them.
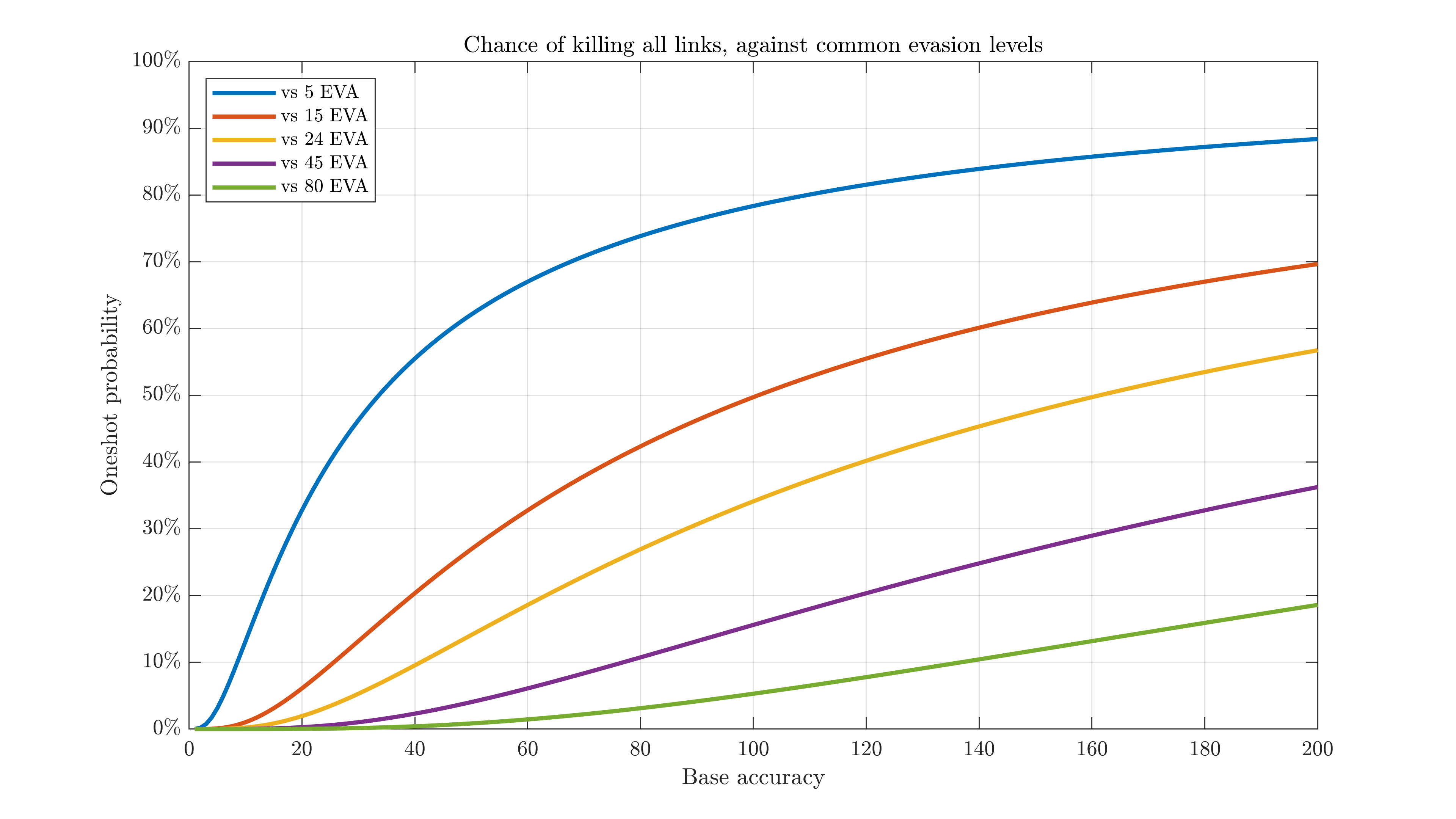
Here are the odds of all shots connecting from a given volley (5 dummies). The x-axis has been expanded to better show the trend, as otherwise even with 100 accuracy you'd only oneshot a 15-evasion enemy ~50% of the time: (100/(100+15))^5=49.7%. Oneshot probability increases much more linearly with typical accuracy values - 80-100 for rifles, before buffs - suggesting that accuracy is more useful to buff if you're fighting low-HP enemies. Of course, ROF is even more valuable in many such situations.
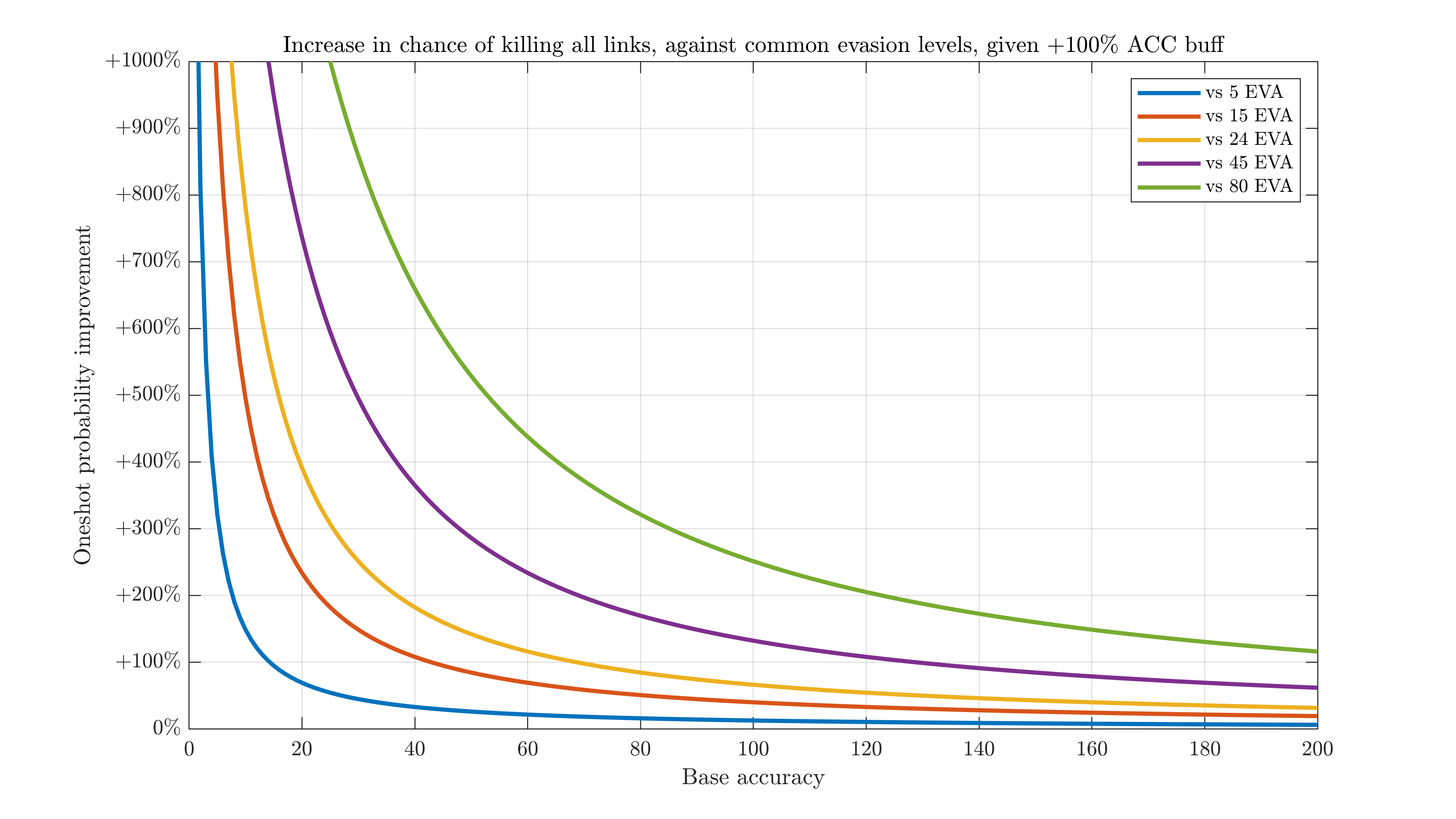
M4-based exodias avoid this problem by having surehit, Type88-based ones by having piercing/multihit. An alternative interpretation of this is that you can't realistically buff acc enough to reliably oneshot evasive enemies, and thus shouldn't build IWS exodias.
Heavy Ordnance Corps#
HOCs have their own accuracy equivalent, precision. It's a similar equation, but with different coefficients and an actual floor:
$$ \mathrm{HOC~hit~rate~(\%)} = \mathrm{max}\left(\frac{\mathrm{Precision}\div 8}{\mathrm{Precision}\div 8+\mathrm{EVA}}\times100\%,~40\%\right) $$where \(\mathrm{max}(a,b)\) returns the higher value between a and b. Visually:
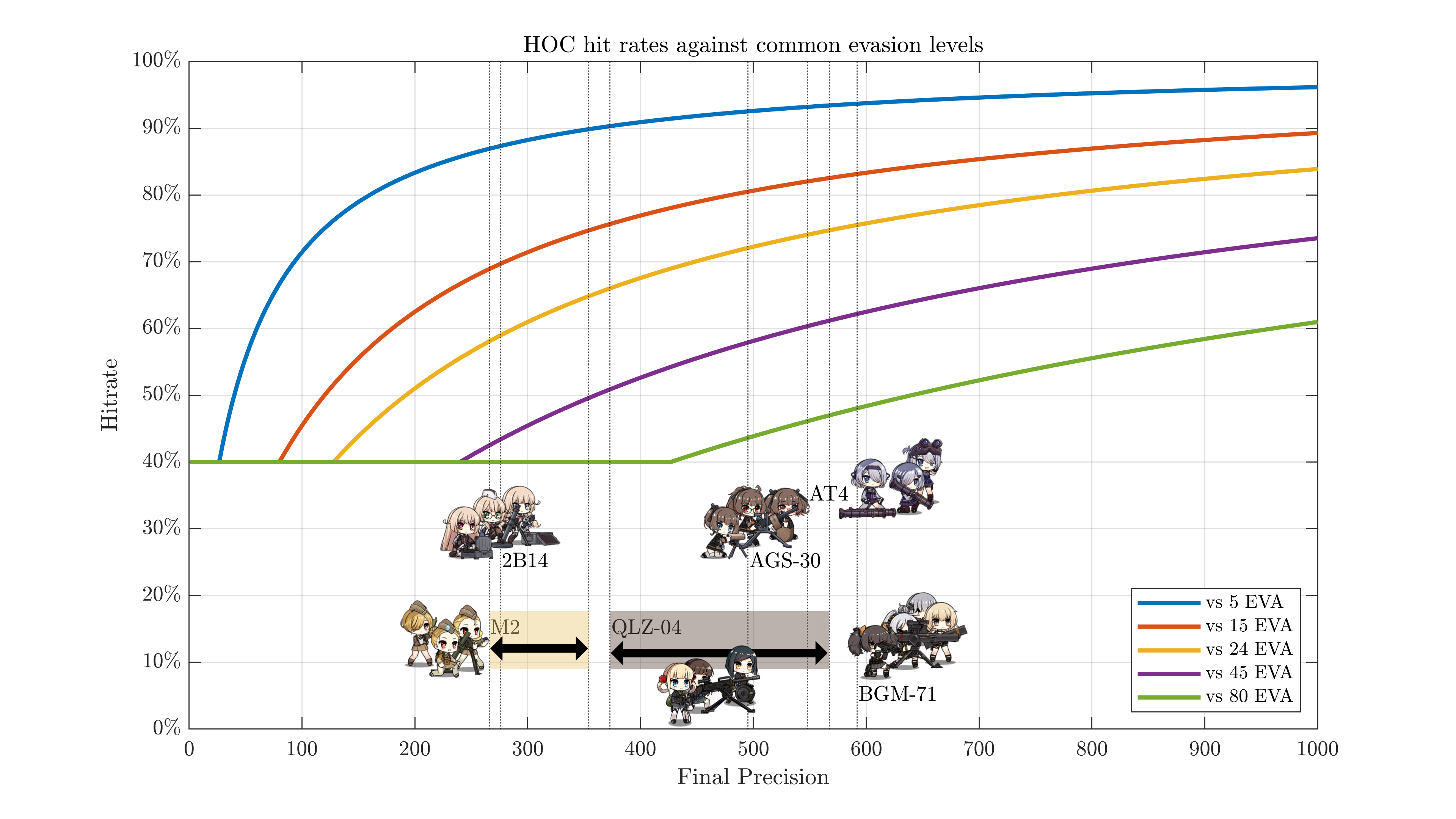
Mk 153 may be added once Theater rewards are distributed and I get her chipped/upgraded. QLZ's evasion debuff is not accounted for here. Stats are based on my personal HOCs, which are at worst ~99.5% optimized. 2B14 uses a lethality/precision preset.
So: low-precision HOCs like 2B14 and M2 may run up against the 40% floor against enemies with 50+ EVA or so. More precise ones will stay above it until a bit past 80 EVA. In most cases, you can expect your HOCs to hit 70-80% of the time.
In conclusion#
Free evasion is never bad, but it's less exciting when you don't have much of it to start with. Luckily, no currently released MGs waste their tilebuff on SG EVA. Killing faster is generally better mitigation than evading harder, so take damage buffs over evasion buffs when possible. If there's minimal opportunity cost, some extra evasion can be very nice in most ARSMG formations, as it will give a solid survivability improvement. Don't sleep on P22's middle column buff, and try to double dip on that & the shields whenever possible.
Having high evasion doesn't mean you can't get hit. Even with a proper evasion stack, it may feel like you're getting hit more than you should. This is to be expected - people are quite bad with probability in general, especially so with extreme numbers. Consider how many people believe XCOM's 95% shots are not actually 95% (they are), just because of a few unlucky times they lost a unit after missing one of those.
On the offensive, the more accuracy the better. Exact thresholds will vary by personal preference, but you can stop worrying once you have a few times more accuracy than your target has evasion.
For more math stuff including things like the reasons flares suck and converting between accuracy debuffs/evasion buffs, this writeup remains an excellent resource.